Перпендикулярная прямая по отношению к плоскости
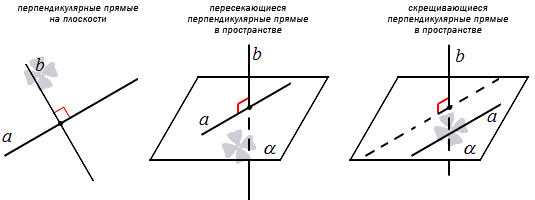
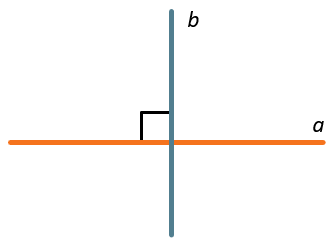
Перпендикулярные прямые на плоскости: определение и доказательство теоремы
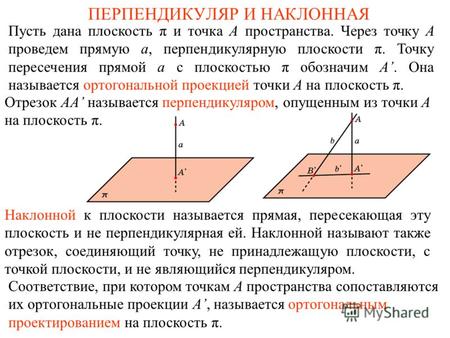
Статья раскрывает понятие о перпендикулярности прямой и плоскости, дается определение прямой, плоскости, графически иллюстрировано и показано обозначение перпендикулярных прямой и плоскости. Сформулируем признак перпендикулярности прямой с плоскостью. Рассмотрим условия, при которых прямая и плоскость будут перпендикулярны с заданными уравнениями в плоскости и трехмерном пространстве.


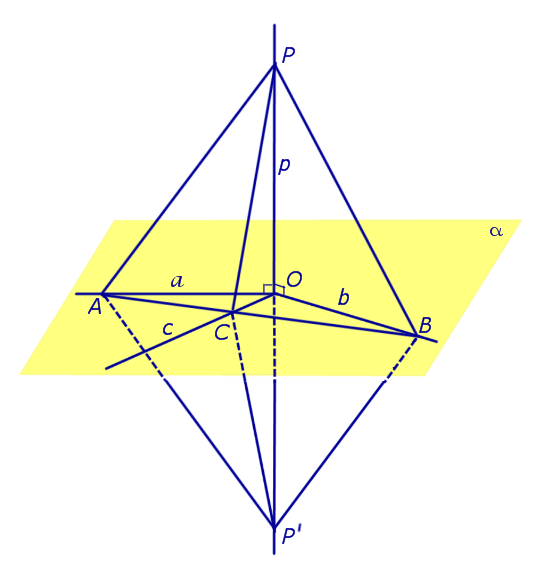
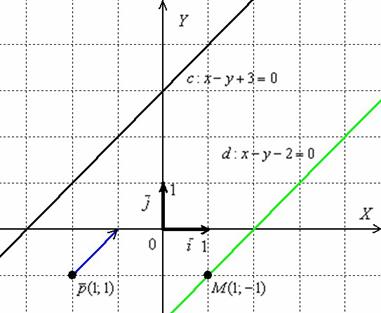

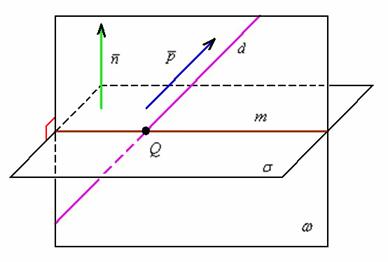



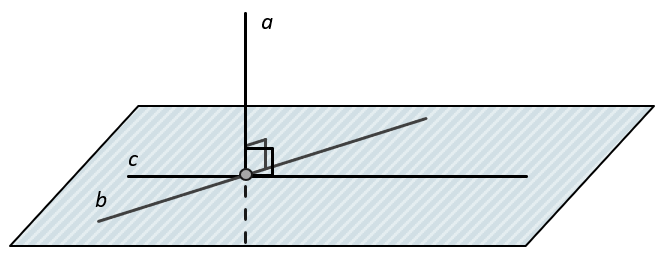
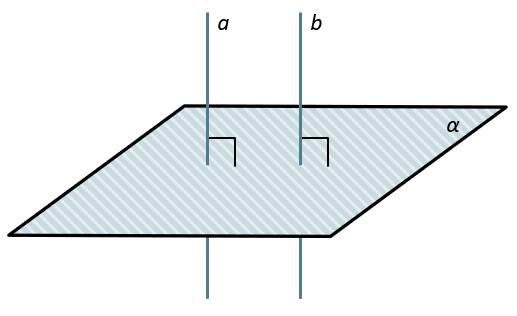
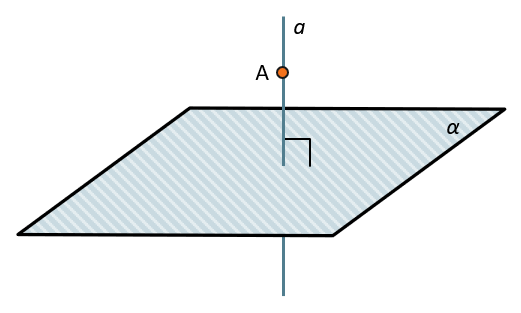
Разделы: Математика , Конкурс «Презентация к уроку». Загрузить презентацию кБ. Цели урока: Обобщение изученного теоретического материала, систематизация его, установление межпредметных связей этого материала, исторические начала, расширение сведений по данной теме, воспитание интереса к данной теме, воспитание интереса и любви к математике. Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Теорема: 1 Если одна из двух параллельных прямых перпендикулярна к Плоскости, то и другая прямая перпендикулярна к этой плоскости.
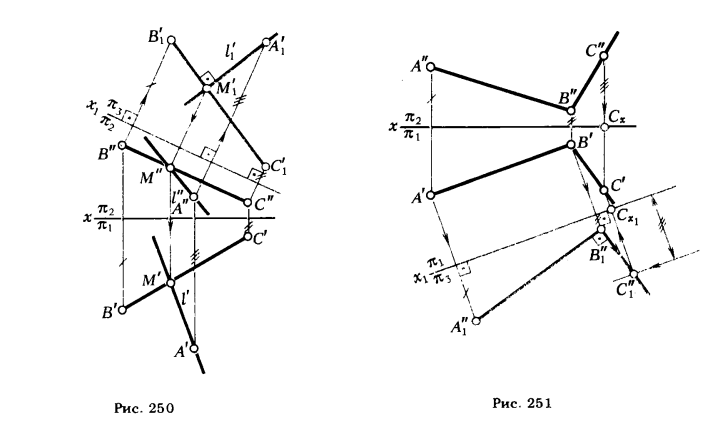
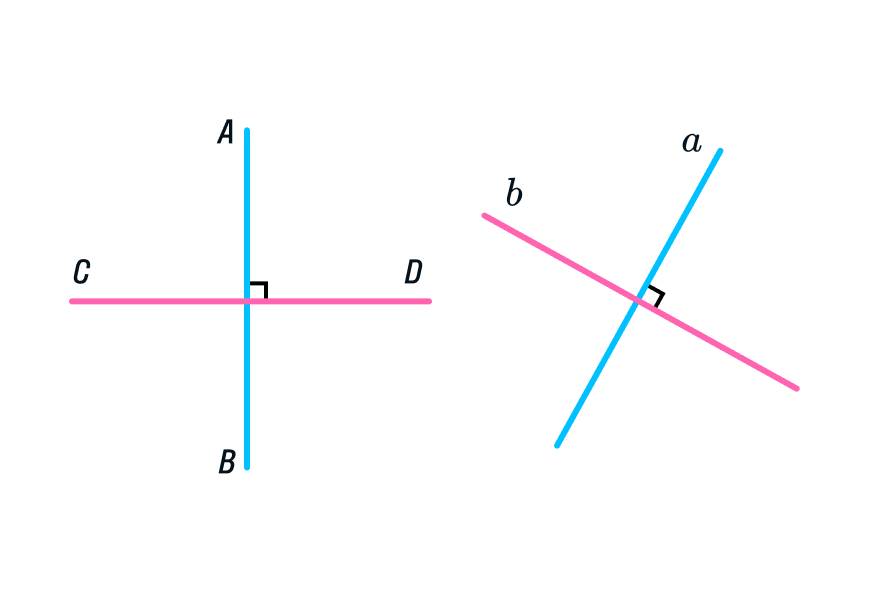
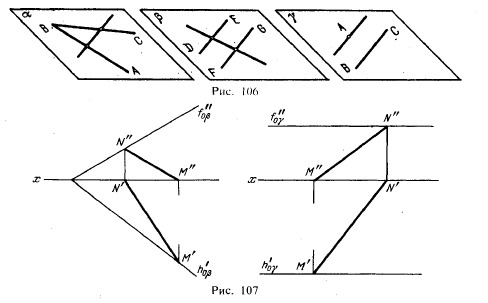






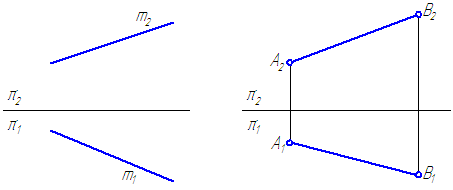
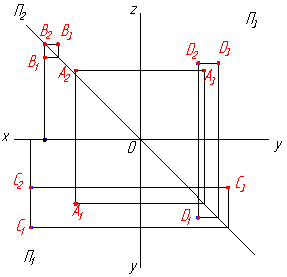
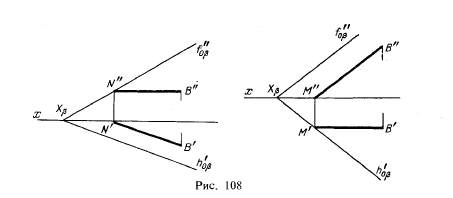
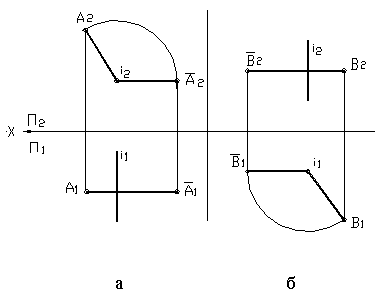
Примеры построения перпендикулярных прямых: а - h; б - f. Для того чтобы эти прямые углы спроецировались в натуральную величину, прямые b и с должны быть параллельны плоскостям проекций, т. При этом прямые углы между прямой а и прямыми h и f на соответствующие плоскости проекций спроецируются без искажений. Изображение прямых, перпендикулярных к плоскостям заданным: а - плоскостью фигуры АВС; б - прямыми c, d. Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы.